यंग का द्विस्लिट प्रयोग क्या है ?

यंग का द्विस्लिट प्रयोग क्या है ?

आज के इस टॉपिक में हम यंग का द्विस्लिट प्रयोग ( Young’s Two-Slit Experiment ) के बारे में समझेंगे जिसमे हम यह देखेंगे की यंग का द्विस्लिट प्रयोग क्या होता है इसका उपयोग किसलिए किया जाता है तथा यह प्रयोग किस प्रकार किया जाता है इस प्रयोग के आधार पर किस प्रकार से फ्रिन्ज की चौड़ाई नापकर प्रकाश की तरंगदेर्ध्य ज्ञात की जा सकती है और किस प्रकार से दीप्त फ्रिन्जों की स्थतियो तथा अदीप्त फ्रिन्जों की स्थतियों का पता लगाया जा सकता है और किस प्रकार से फ्रिंज चौड़ाई ज्ञात की जा सकती है |

इन सभी बिन्दुओं पर चर्चा करेंगे तो चलिए समझना शुरू करते है की यंग का द्विस्लिट प्रयोग क्या होता है और किस प्रकार यह प्रयोग किया जाता है

यंग का द्विस्लिट प्रयोग

यंग का द्विस्लिट प्रयोग मुख्य रूप से व्यतिकरण की घटना की व्याख्या करता है जिसको समझाने के लिए वैज्ञानिक थॉमस यंग ने सन 1802 में एक प्रयोग किया जिसमे प्रकाश स्त्रोत से निकलने वाली तरंगो से उत्पन्न व्यतिकरण की घटना की Study की और अपने प्रयोगों के आधार पर कुछ Results दिए इसे ही यंग का द्विस्लिट प्रयोग कहा जाता है |

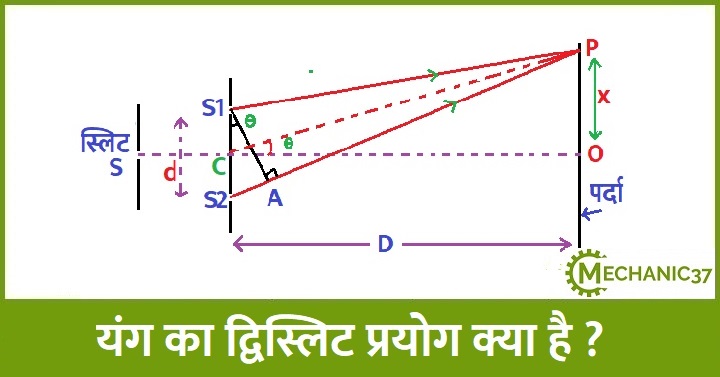
यह प्रयोग करने के लिए यंग ने एक स्लिट ली जिसे लगभग 1 mm की चोड़ाई की रखी और इसे S नाम दिया अब इस स्लिट पर प्रकाश के किसी स्त्रोत से प्रकाश डाला गया तथा स्लिट S से कुछ दूरी पर ( लगभग 10 Cm ) S के समांतर स्लिट S1 तथा S2 को रखा गया और इसके बाद इन स्लिट S1 तथा S2 से कुछ दूरी पर एक पर्दा रखा गया जिसे XY नाम दिया गया |

अब इस तरह से जब पूरा परिपथ तैयार करके जब प्रयोग किया गया तो उसमे कुछ परिणाम निकलकर सामने आये जो की इस प्रकार थे –

1 . जो पर्दा लगा रहता है उस पर कुछ चमकीली पट्टियाँ प्राप्त होती है जिन्हें दीप्त फ्रिन्जें कहा जाता है तथा कुछ काली पट्टियाँ प्राप्त होती है जिन्हें अदीप्त फ्रिन्जें कहा जाता है  | तथा ये दीप्त फ्रिन्जें एवं अदीप्त फ्रिन्जें एकान्तर क्रम में प्राप्त होती है और जब एकान्तर क्रम में दीप्त फ्रिन्जें एवं अदीप्त फ्रिन्जें प्राप्त होती है तो इन फ्रिन्जों के समुह को ही व्यतिकरण प्रतिरूप कहा जाता है |

2 . पर्दे पर प्राप्त सभी चमकीली पट्टियों अर्थात दीप्त फ्रिन्जो की तीव्रता तथा सभी काली पट्टियों अर्थात अदीप्त फ्रिन्जों की तीव्रता एक समान रहती है जिनमे से दीप्त फ्रिन्जों की तीव्रता अधिकतम होती है और अदीप्त फ्रिन्जों की तीव्रता न्यूनतम या लगभग शून्य होती है |

3 . साथ ही साथ यह भी देखा गया की पर्दे पर प्राप्त किन्ही भी दो चमकीली या दीप्त फ्रिन्जों या फिर किन्ही भी दो काली या अदीप्त फ्रिन्जों के बीच की की दूरी एक समान रहती  है और इसी दूरी को फ्रिन्जं की चौड़ाई भी कहा जाता है |

4 . सभी दीप्त और अदीप्त फ्रिन्जों की चौड़ाई एकसमान होती है |

इस प्रकार ये कुछ Results थे जो की यंग का द्विस्लिट प्रयोग के आधार पर प्राप्त हुए |

अब हम यह समझेंगे की यंग का द्विस्लिट प्रयोग के आधार पर किस प्रकार से फ्रिन्ज की चौड़ाई नापकर प्रकाश की तरंगदेर्ध्य ज्ञात की जा सकती है और किस प्रकार से दीप्त फ्रिन्जों की स्थतियो तथा अदीप्त फ्रिन्जों की स्थतियों का पता लगाया जा सकता है और किस प्रकार से फ्रिंज चौड़ाई ज्ञात की जा सकती है |

फ्रिन्ज की चौड़ाई नापकर प्रकाश की तरंगदेर्ध्य ज्ञात करना

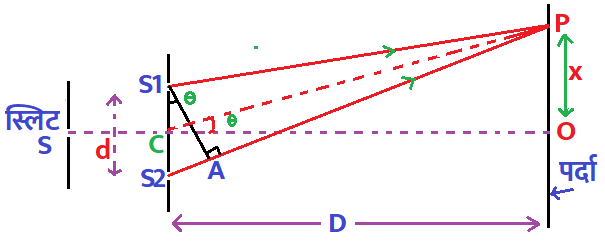
जैसा की चित्र में दिखाया गया है की स्लिट S पर प्रकाश के किसी स्त्रोत से प्रकाश डाला गया तथा स्लिट S से कुछ दूरी पर स्लिट S1 तथा S2 को रखा गया और इसके बाद इन स्लिट S1 तथा S2 से कुछ दूरी पर एक पर्दा रखा गया जिसे XY नाम दिया गया तथा मानाकि स्लिट S1 तथा S2 के बीच की दूरी d है तथा S1 तथा S2 से पर्दे की दूरी D है तब पर्दे पर प्राप्त किसी बिंदु P पर –

S2P – S1P = S2A

अब ΔS1S2A तथा PCO में

S2A/S1S2 = OP/CP

लेकिन जब CO , S1S2 की तुलना में बड़ी हो तब CP=CO

S2A/S1S2 = OP/CO

S2A/d = x /D

तथा पथांतर S2A = xd /D

अब हम समझते है दीप्त फ्रिन्जों की स्थतियों के बारे में

दीप्त फ्रिन्जों की स्थतियां

यह बात हम पहले ही समझ चुके है की दीप्त फ्रिन्जो पर तीव्रता अधिकतम होती है और जहाँ तीव्रता अधिकतम होती है उन बिन्दुओं के बिच पथांतर कुछ इस प्रकार होता है 0 , λ,2λ…..आदि

इसका मतलब यह हुआ की  

xd /D = kλ

जहाँ k का मान 0 ,1 ,2 …… है |

अदीप्त फ्रिन्जों की स्थतियां

यह भी हम पहले समझ चुके है की अदीप्त फ्रिन्जों पर प्रकाश की तीव्रता न्यूनतम होती है तथा जहाँ तीव्रता न्यूनतम होती है उन बिन्दुओ पर पथांतर कुछ इस प्रकार होता है λ/2,3λ/2,5λ/2 ….आदि |

इसका मतलब यह हुआ की  

xd /D = (k-1 /2 )λ

जहाँ k का मान 1 ,2,3 …… है |

फ्रिन्ज चौड़ाई

जैसा की हमने पहले समझा था की किन्ही भी दो क्रमागत दीप्त फ्रिन्जो के बीच की दूरी को फ्रिंज चौड़ाई कहा जाता है और इसे w से दर्शाया जाता है अर्थात

w = Dλ/d

जहाँ D = स्लिट से पर्दे के बीच की दूरी है तथा

d = स्लिटों S1 तथा S2 के बीच की दूरी है |