बायो सेवर्ट का नियम क्या है ? स्टेटमेंट , डेरीवेशन एव उपयोग समझाइये
बायो सेवर्ट का नियम
आज के इस टॉपिक में बायो सेवर्ट के नियम के बारे में पड़ेंगे जो किसी कंडक्टर में उत्पन्न होने वाले चुम्बकीय क्षेत्र के बारे में बताता है | इसके लिए हम एक कंडक्टर लेते है तथा उसमे विद्युत धारा ( करंट ) प्रवाहित करते है | अब इसके बाद इस कंडक्टर में होने वाले उत्पन्न चुम्बकीय क्षेत्र के बारे में अध्ययन किया जाता है | यही अध्ययन इस नियम के अंतर्गत आता है | तो अब हम इसके बारे में डिटेल में पड़ते है |
इस नियम के अनुसार किसी कंडक्टर से धारा प्रवाहित करने से उसके चारो और उत्पन्न चुम्बकीय क्षेत्र की तीव्रता उस कंडक्टर से बहने वाली करंट , उस कंडक्टर पर लिए गये अल्पांश तथा कंडक्टर से बिंदु को मिलाने वाली रेखा के कोण के समानुपाती होती है तथा उस कंडक्टर से बिंदु की दूरी के वर्ग के व्युत्क्रमानुपाती होती है | यही बायो सेवर्ट का नियम होता है |
लेकिन इस नियम के बारे में पड़ने से पहले हमें इस बात का पता होना चाहिए की जब भी हम किसी कंडक्टर से होकर करंट प्रवाहित करते है , तो उस कंडक्टर के चारो और चुम्बकीय क्षेत्र ( मैग्नेटिक फील्ड ) उत्पन्न हो जाता है | और यह मैग्नेटिक फील्ड गोलाकार आकृति का होता है |
अब इस मैग्नेटिक फील्ड में इस कंडक्टर पर एक बल भी लगता है जिसे मैग्नेटिक बल कहा जाता है , अब इस मैग्नेटिक फील्ड में किसी एक बिंदु पर मैग्नेटिक फील्ड ज्ञात करके उसकी सहायता से पूरे कंडक्टर का मैग्नेटिक फील्ड निकाला जाता है किसी भी स्थान पर एक बिंदु की कल्पना की जाती है | इस बिंदु पर चुम्बकीय क्षेत्र की तीव्रता निकाली जाती है | इसके लिए कंडक्टर को छोटे – छोटे अल्पांश में बांट दिया जाता है |
अब इस एक छोटे अल्पांश से किसी बिंदु पर चुम्बकीय क्षेत्र की तीव्रता निकाल ली जाती है | और फिर सभी अल्पांश का चुम्बकीय क्षेत्र ( मैग्नेटिक फील्ड ) जोड़ दिया जाता है , जिससे पूरे कंडक्टर का मैग्नेटिक फील्ड ज्ञात किया जा सकता है |
बायो सेवर्ट का सूत्र तथा डेरिवेशन
बायो सेवर्ट के नियम का कथन ही यही है की किसी करंट Carrying कंडक्टर के एक छोटे से अल्पांश से किसी स्पेसिफिक पॉइंट पर यदि विद्युत क्षेत्र की तीव्रता निकाली जाए तो वह किस – किस पर निर्भर करती है और किस प्रकार निर्भर करती है |
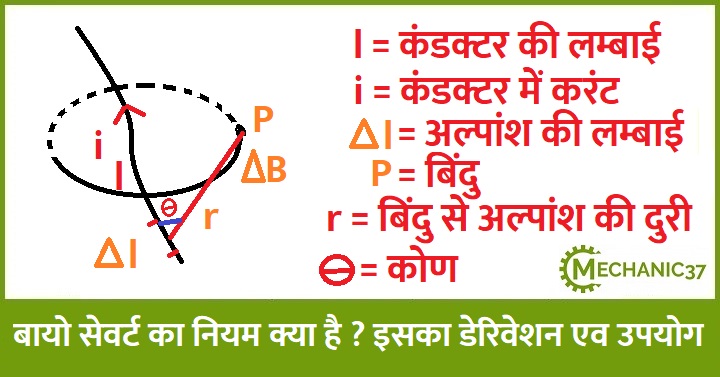
हम कल्पना करते है की कोई एक कंडक्टर है जिससे होकर करंट प्रवाहित हो रही है तथा जिसकी लम्बाई l है , तथा इससे होकर i करंट प्रवाहित हो रही है | अब यदि इस कंडक्टर से r दुरी पर इस कंडक्टर के चुम्बकीय क्षेत्र में कोई एक बिंदु p की कल्पना की जाती है |
तथा l लम्बाई के कंडक्टर में एक अल्पांश लिया जाए जिसकी लम्बाई ∆l है , तथा यह बिंदु p कंडक्टर से ɵ कोण बनाए हुए है | अब यदि r दूरी पर स्थित बिंदु p पर चुम्बकीय क्षेत्र की गणना की जाए तो वह निचे दिए गए कथनों के अनुसार निर्भर करती है |
इस नियम के अनुसार यदि किसी कंडक्टर से होकर करंट प्रवाहित की जाती है तो इस कंडक्टर के चारो और किसी बिंदु p पर उत्त्पन्न होने वाले चुम्बकीय क्षेत्र की तीव्रता ∆B निम्नलिखित बातो पर निर्भर करती है –
1 . चुम्बकीय क्षेत्र की तीब्रता ∆B उस कंडक्टर में बहने वाली करंट i के समानुपाती होती है
अर्थात ∆B ∝ i
2 . चुम्बकीय क्षेत्र की तीव्रता ∆B कंडक्टर के अन्दर लिए गए अल्पांश की लम्बाई ∆l के भी समानुपाती होती है
अर्थात ∆B ∝ ∆l
3 . चुम्बकीय क्षेत्र की तीव्रता ∆B , अल्पांश ∆l से बिंदु p को मिलाने वाली रेखा के कोण की ज्या ( sin ɵ ) के भी समानुपाती होती है
अर्थात ∆B ∝ sin ɵ
4 . चुम्बकीय क्षेत्र की तीव्रता ∆B , उस कंडक्टर के अल्पांश ∆l से बिंदु p को मिलाने वाली दूरी के वर्ग के व्युत्क्रमानुपाती होती है
अर्थात ∆B ∝ 1 / r2
इस प्रकार बायो सेवर्ट के नियम के अनुसार दिए गए चारो कथनों को यदि एकसाथ मिला दिया जाए और एक साथ सभी कथनों को लिखा जाए तो इस प्रकार होगा –
अर्थात ∆B ∝ ( i ∆l sin ɵ ) / r2
या फिर अगर समानुपाती के चिन्ह को हटाया जाए तो यहाँ एक नियतांक ( Constant ) का उपयोग किया जाएगा जिसे हम k नाम से जानते है
अर्थात ∆B = k ( i ∆l sin ɵ ) / r2
तथा यहाँ k एक नियतांक है जिसका मान µ ₀ / 4 ∏ होता है
अर्थात यदि इस समीकरण में k का मान रख दिया जाए तो प्राप्त समीकरण कुछ इस प्रकार होगा –
अर्थात ∆B = µ ₀ ( i ∆l sin ɵ ) / 4 ∏ r2
जहा µ ₀ को निर्वात की चुम्बकशीलता कहा जाता है |
तथा µ ₀ / 4 ∏ का मान 10 ꣻ ⁷ होता है तथा इसकी इकाई N / A2 होती है |
यही बायो सेवर्ट का नियम तथा उसका डेरिवेशन होता है |
अब ऊपर दिए गए सूत्र से हमे पता चलता है की चुम्बकीय क्षेत्र की तीव्रता ∆B , अल्पांश ∆l से बिंदु p को मिलाने वाली रेखा के कोण की ज्या ( sin ɵ ) के भी समानुपाती होती है अर्थात ∆B समानुपाती sin ɵ अब इसका मतलब यह हुआ की अगर यह बिंदु p अल्पांश से 90 डीग्री का कोण बनाए तब बिंदु p अल्पांश के साथ एक सीधी रेखा में होगा तब चुम्बकीय क्षेत्र की तीव्रता ∆B का मान अधिकतम होगा |
और जैसे – जैसे ɵ का मान कम होता जाएगा | चुम्बकीय क्षेत्र की तीव्रता ∆B का मान भी कम होगा और यदि ɵ का मान जीरो हो गया अर्थात बिंदु p कंडक्टर के ऊपर ही आ गया तो इस स्थति में चुम्बकीय क्षेत्र की तीव्रता ∆B का मान भी जीरो हो जाएगा |
बायो सेवर्ट का नियम के उपयोग
1 . इस नियम का उपयोग करके आण्विक तथा परमाण्विक लेवल के मैग्नेटिक रिएक्शन की भी गणना आसानी के साथ की जा सकती है |
2 . इसका उपयोग वेलोसिटी Encouraged With Vortex लाइन के लिए एयरोडायनामिक थ्योरी के लिए इनका उपयोग किया जाता है |
3 . किसी करंट एलिमेंट के द्वारा मैग्नेटिक फील्ड की गणना के लिए भी इनका उपयोग किया जाता है |
4 . इस नियम का उपयोग करके किसी सर्कुलर Coil , डिस्क , लाइन सेगमेंट आदि के द्वारा मैग्नेटिक फील्ड ज्ञात किया जा सकता है |

Leave a Reply