गियर और पिनियन अरेंजमेंट और रैक और पिनियन अरेंजमेंट का डेरिवेशन क्या होता है ?
इस पेज पर हम डेरिवेशन को समझेंगे गियर और पिनियन अरेंजमेंट में और रैक और पिनियन अरेंजमेंट में | इसमें सबसे पहले न्यूनतम टीथ की आवश्यकता इन्टरफेरेंस से बचने के लिए पिनियन और गियर पर निकालेंगे उसके बाद रैक एंड पिनियन अरेंजमेंट में न्यूनतम टीथ की आवश्यकता इन्टरफेरेंस को दूर करने के लिए डिफाइन करेंगे चित्र के माध्यम से |
गियर और पिनियन अरेंजमेंट
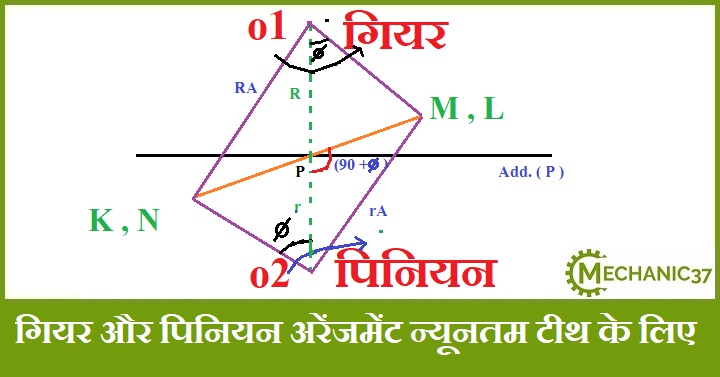
त्रिकोण ΔO2 PL में –
cos rule –
ra2 = r2 + R2 sin 2 ɸ – 2 (r) (R sin ɸ) cos ( 90 + ɸ )
= r2 + ( R2 + 2 rR) sin 2 ɸ
= r2 [ 1 + (R/r).(R/r) + 2 ) sin 2 ɸ]
rA = r √[ 1 + G ( G+2 )sin 2 ɸ]
G = R/r = गियर अनुपात
Addendum ( पिनियन का ) = rA – r
rA – r = r [√[ 1 + G ( G+2 )sin 2 ɸ] – 1 ]
m t mini/2 [√[ 1 + G ( G+2 )sin 2 ɸ] – 1 ] = m Ap
m = Module
Ap = Addendum Distance पिनियन का |
न्यूनतम टीथ इन्टरफेरेंस से बचने के लिए पिनियन और गियर पर
t mini = 2 Ap / [√[ 1 + G ( G+2 )sin 2 ɸ] – 1 ]
न्यूनतम टीथ गियर पर
t mini = 2 AG / [√[ 1 + 1 /G ( 1 /G+2 )sin 2 ɸ] – 1 ]
AG = Addendum Distance गियर का
रैक एंड पिनियन अरेंजमेंट में न्यूनतम टीथ की आवश्यकता इन्टरफेरेंस को दूर करने के लिए
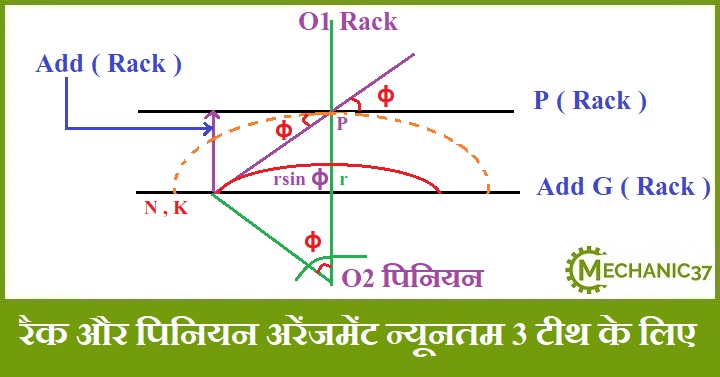
sin ɸ = Addendum / r sin ɸ ( रैक का )
Addendum ( रैक ) = r sin 2 ɸ
= m t mini/2 sin 2 ɸ = m AR
m = मोडियुल
AR = रैक का Addendum
न्यूनतम टीथ t mini = 2 AR / sin 2 ɸ
यह न्यूनतम टीथ केवल और केवल रैक और पिनियन कैश में Valid है |

Leave a Reply